Collatz Problem (3n+1 Problem)

The Collatz problem, also known as 3n+1 problem, is a problem posed by the German mathematician Lothar Collatz in 1937 at the University of Hamburg: Does the Hailstone sequence always terminate (i.e. end in 1) for any value of n?

Hailstone Sequence

A 'Hailstone' sequence is defined as: For any positive integer, the next item in the sequence is obtained by dividing the number by 2 if the number is even, otherwise multiply it by 3 and add 1. Expressing this as a function:

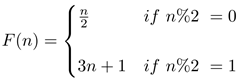
Consider, for instance, n=24 the generated iterates are: {24, 12, 6, 3, 10, 5, 16, 8, 4, 2, 1}. Notice that the sequence settled into a three-number cycle: 1, 4, 2. This repeats forever.

Collatz Conjecture

The conjecture states that for any positive integer n, the Hailstone Sequence
will eventually reach the number 1. Note that, although Collatz problem is based on this simple concept, it is intractably hard.

Until today, nobody has been able to prove it! this is why it is call a conjecture, which means it hasn't been proven true. So far, it has been verified for n <= 5.48e18 by Leaven and Vermeluen. This name is a big one, so by empirical reasoning, it would be safe to say that the Collatz conjecture is true. But this is not a mathematical proof (Just because the Collatz conjecture has been verified for the first N numbers, there's nothing stopping it from failing at number N+1)

Sample Code

The following sample code (Java and Python) asks the user for a positive integer and prints the Hailstone sequence among it's length and maximum value.

Java

public class CollatzProblem {

    public static void main(final String[] args) {
        final Scanner scanner = new Scanner(System.in);
        while(true){
            System.out.print("\n\nSelect a positive integer: ");
            int n = scanner.nextInt();
            printHailstone(n);
        }
    }

    /**
     * Print the terms, length and maximum value of the 
     * 'hailstone sequence' from n to 1
     *
     * @param n The starting point of the hailstone sequence
     */
    public static void printHailstone(int n) {
        int count = 1;
        int maxValue = n;

        System.out.print("\n[");
        while (n > 1) {
            System.out.print(n + ", ");
            count++;
            n = n % 2 == 0 ? n / 2 : 3 * n + 1;
            maxValue = Math.max(n, maxValue);
        }

        System.out.printf(
           "1]\nSequence length: %d\nMaximum value: %d",
           count, maxValue);
    }
}

Python

def hailstone(n):
    """
    Print the terms, length and maximum value of the 'hailstone 
    sequence' from n to 1
    
    :param n: The starting point of the hailstone sequence
    :type n: int
    """
    
    assert n > 0
    count = 1;
    maxValue = n;

    while n>1:
        print(n, end=",")
        count += 1
        n = 3*n + 1 if n & 1 else n//2
        maxValue = max(n, maxValue)

    print(1)
    print("Sequence length:", count);
    print("Maximum value:", maxValue);


if __name__ == '__main__':
    n = int(input("Select a positive integer: "))
    hailstone(n)